今天开始学习算法和设计模式
主要学习资料是
视频 Hua Hua
博客 Huahua’s Tech Road
#20200418
学习了并查集,看了视频
花花酱 Disjoint-set/Union-find Forest - 刷题找工作 SP1 , 博客文章
视频里面主要讲了 find 和 union 两个操作。
find 即找到节点的root。 对应路径压缩。 这里面有个点是,路径压缩是在find 的过程中进行的,如果不进行find,则不进行路径压缩。并且具体实现是通过递归实现。具体实现 我不太会用语言描述,主要是对递归的理解不深。递归算法需要加强下
union 对应分枝合并,将 rank 少的合并到 rank 多的。
并查集 这个算法 在 算法(第4版) [Algorithms Fourth Edition] 这本书里面是单独的一个章节 还需要详细学习下。。
参考链接
https://www.cs.princeton.edu/courses/archive/spring13/cos423/lectures/UnionFind.pdf
#20200425
根据数据输入规模估算时间复杂度,从而大概找到对应的算法。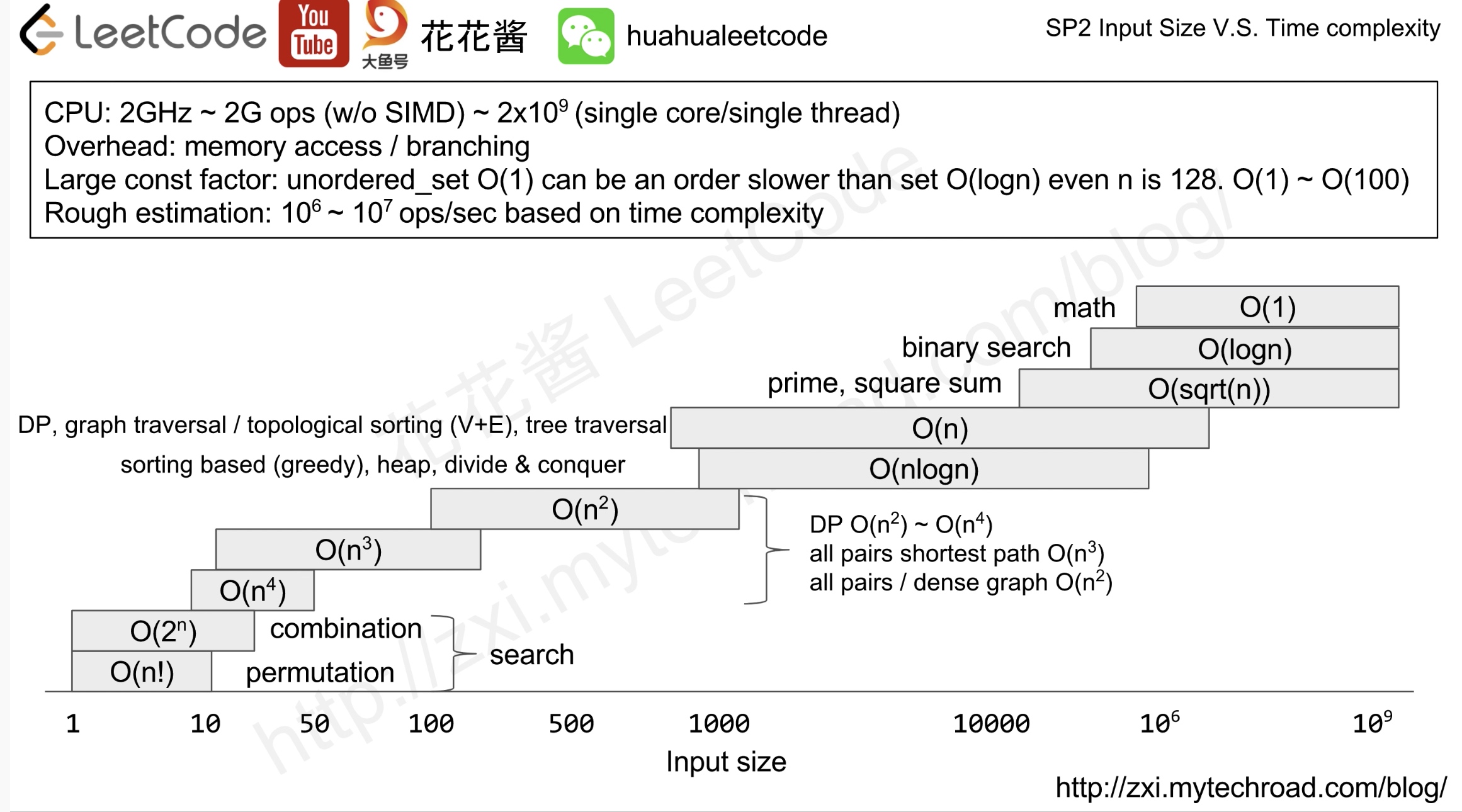
树状数组 (没搞懂,找别的资料看一下)

线程与进程
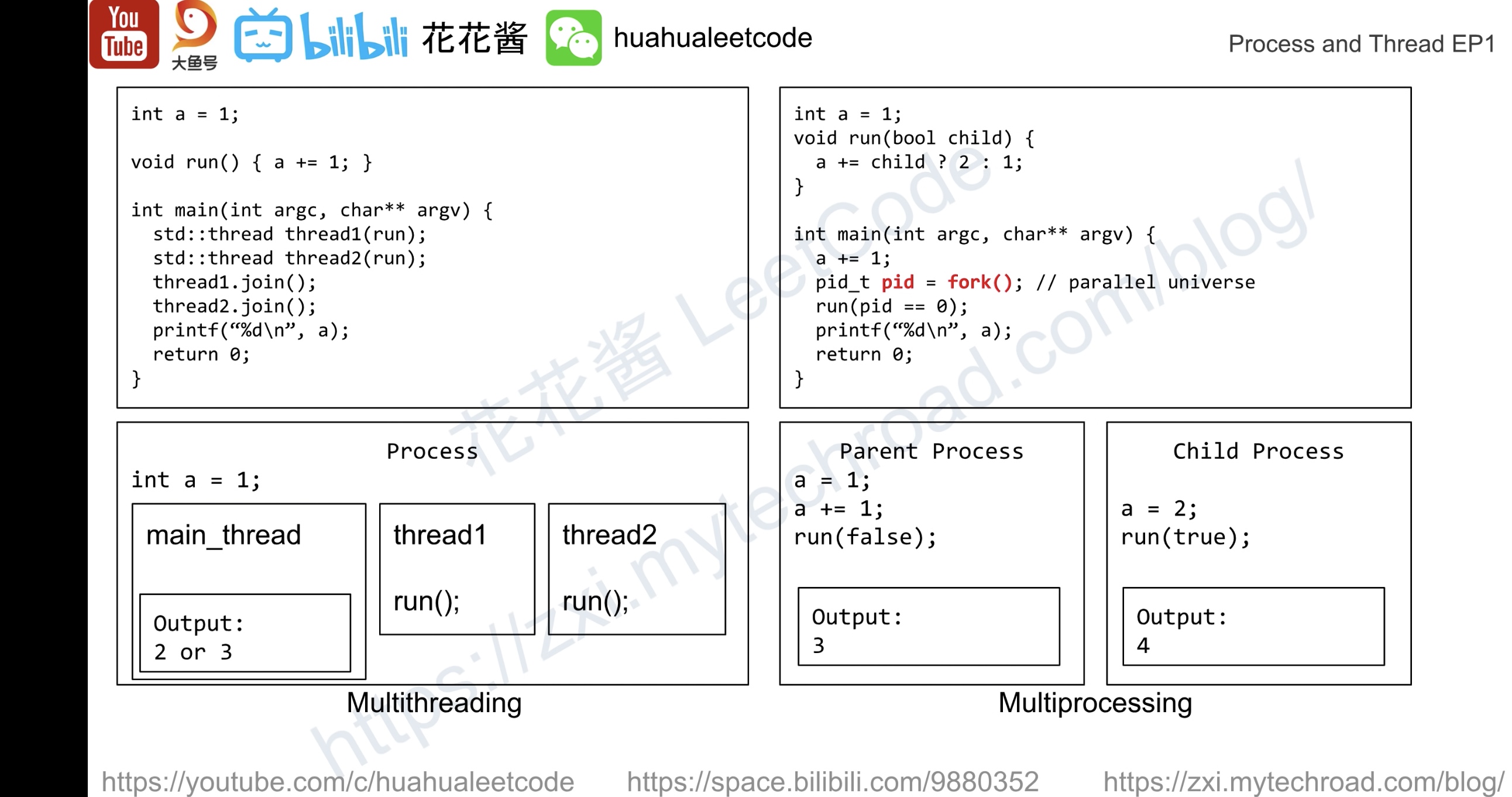
#20200512
#正则表达式入门
A.*A 字符串中有两个ALLL 字符串中有连续三个LA.*A|LLL 字符串中有两个A 或者连续的三个L
正则表达式的优势 是 可读性高。
#动态规划入门
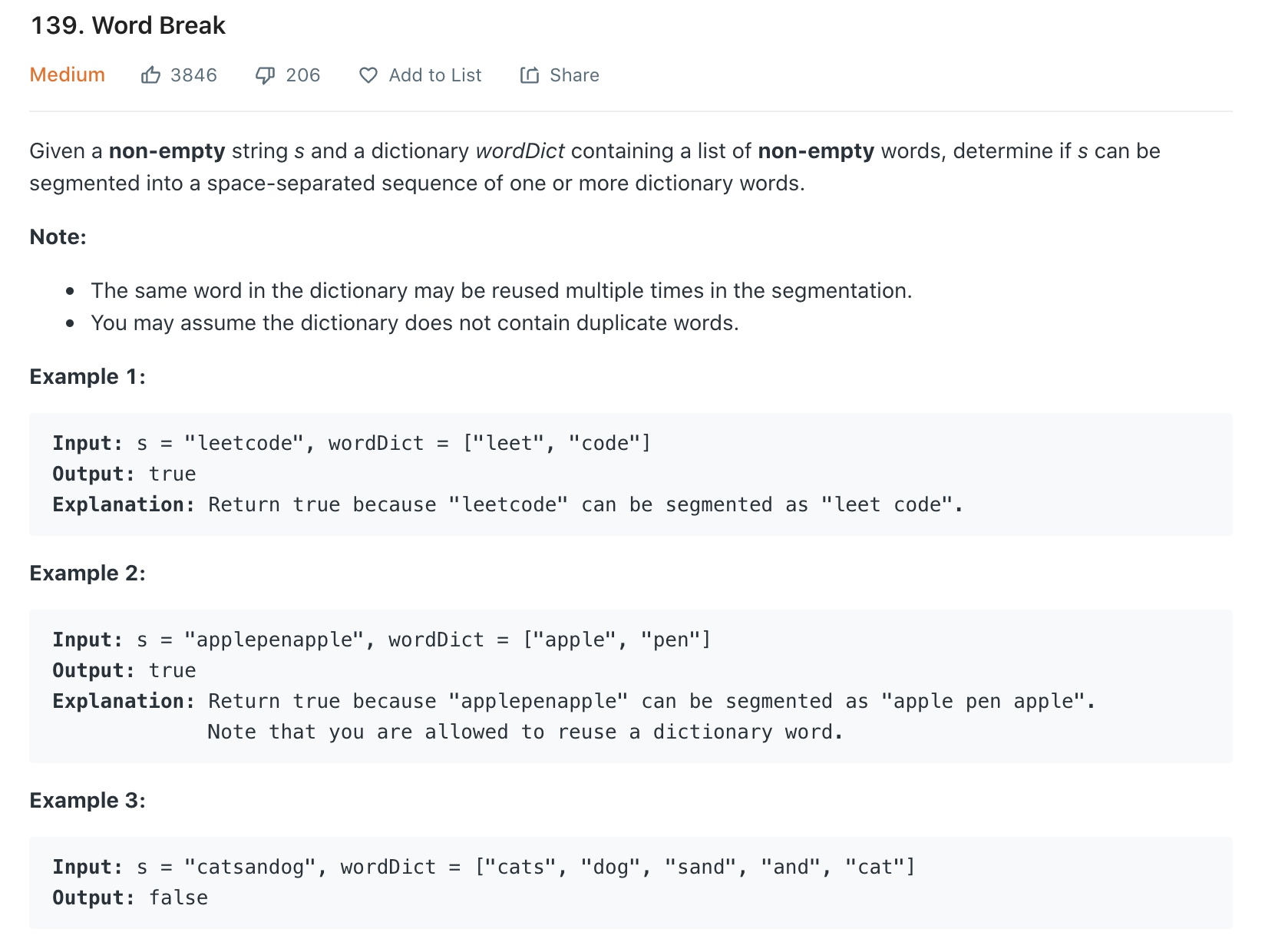
这个题目的思路是找到中间节点 如果前i的子串中间节点右边的串在字典中 ,那么前i的子串就是可分割的。
整个字符串是否可分割即 i 等于 字符串长度 时是否能找到中间节点右边的串在字典中。
这里先是在 s 前加了一个空字符。
然后构造了长度为n+1,初始值为0的数组,标记 s 前 i 长度的字符串是否可以被分割。
f[0] = 1 的意思是 s 是空字符串。
两层循环。
外层循环是整个问题的规模。即s 的长度。
内层循环是子问题,j 从 0 到 i。如果j 右边到i 的字符串在字典中,即 s[0:i]是可以被分割的。就可以跳出内层循环了。
逐步扩大求解范围,通过解决子问题,从而得到整体问题的解。
#20180718_771 Jewels and Stones
- question
You’re given strings J representing the types of stones that are jewels, and S representing the stones you have. Each character in S is a type of stone you have. You want to know how many of the stones you have are also jewels.
The letters in J are guaranteed distinct, and all characters in J and S are letters. Letters are case sensitive, so “a” is considered a different type of stone from “A”.
Example 1:
1 | Input: J = "aA", S = "aAAbbbb" |
Example 2:
1 | Input: J = "z", S = "ZZ" |
- solution
1 | class Solution(object): |
#20180719_709 To Lower Case
- question
Implement function ToLowerCase() that has a string parameter str, and returns the same string in lowercase.
Example 1:
1 | Input: "Hello" |
Example 2:
1 | Input: "here" |
Example 3:
1 | Input: "LOVELY" |
- solution
1 | class Solution(object): |
#20180720_595 Big Countries
- question
There is a table World
1 | +-----------------+------------+------------+--------------+---------------+ |
A country is big if it has an area of bigger than 3 million square km or a population of more than 25 million.
Write a SQL solution to output big countries’ name, population and area.
For example, according to the above table, we should output:
1 | +--------------+-------------+--------------+ |
- solution
1 | # Write your MySQL query statement below |
#20180721_804 Unique Morse Code Words
- question
International Morse Code defines a standard encoding where each letter is mapped to a series of dots and dashes, as follows: “a” maps to “.-“, “b” maps to “-…”, “c” maps to “-.-.”, and so on.
For convenience, the full table for the 26 letters of the English alphabet is given below:
1 | [".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."] |
Now, given a list of words, each word can be written as a concatenation of the Morse code of each letter. For example, “cab” can be written as “-.-.-….-“, (which is the concatenation “-.-.” + “-…” + “.-“). We’ll call such a concatenation, the transformation of a word.
Return the number of different transformations among all words we have.
1 | Example: |
There are 2 different transformations, “–…-.” and “–…–.”.
Note:
1 | 1. The length of words will be at most 100. |
- solution
1 | class Solution(object): |
#20180722_461 Hamming Distance
- question
The Hamming distance between two integers is the number of positions at which the corresponding bits are different.
Given two integers x and y, calculate the Hamming distance.
Note:
0 ≤ x, y < 231.
Example:
1 | Input: x = 1, y = 4 |
The above arrows point to positions where the corresponding bits are different.
- solution
1 | class Solution(object): |